ElixirConfEU - Elixir Processes in 3D
I gave a lightning talk at ElixirConfEU on Visualizing Elixir Processes in 3D.

A few nights before travelling to Krakow I had watched a video by Kresten Krab Thorup on his project Erlubi which transmits basic details of the Erlang VM to a Ubigrpah Server.
I started to use this to inspect Erlang projects, and play about with OTP Supervisor trees and how they looked in 3D.
I decided to go about using this from elixir. It doesn’t take much to use from elixir; if you want to visualize your own project simply cherry pick the steps 1, 3, 6 and 7 below.
1 Download the Ubigraph server from ubietylab.net. Unpack it and just run the command line tool bin/ubigraph_server. A black window will appear.
2 Create a new elixir project mix new lightning_ex and cd into directory.
3 Add Erlubi as a dependency to the mix.exs file:
1 2 3 | |
4 Add some code to ex_lightning.ex to generate linked and unlinking procs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
5 In terminal fetch dependencies and compile with mix do deps.get, compile
6 In terminal start an iex session with mix iex -S mix
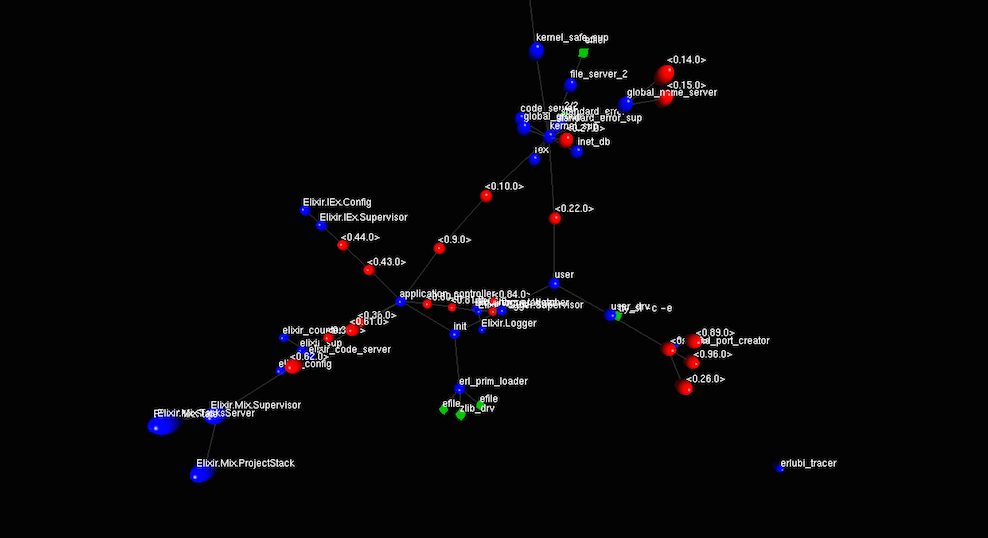
7 In iex session start Erlubi tracer with :erlubi_tracer.run. If you get an error ensure you started ubigraph_server as described in step 1. At this point you should see the vanilla elixir system visualized in 3D like so:
- Green Cubes = Erlang Ports
- Red Spheres = Erlang Processes
- Blue Sphere = Named Erlang Processes
- Grey Line = Process Links
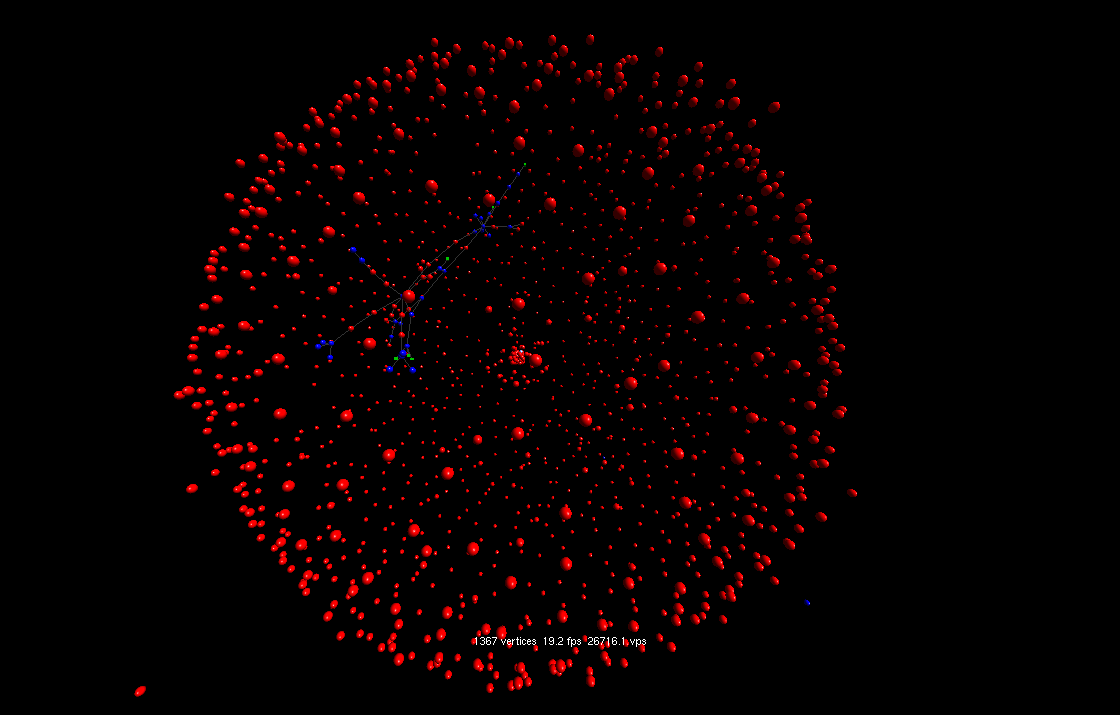
8 run ExLightning.start 5000 which will create 5000 unlinked processes (unbound red spheres)
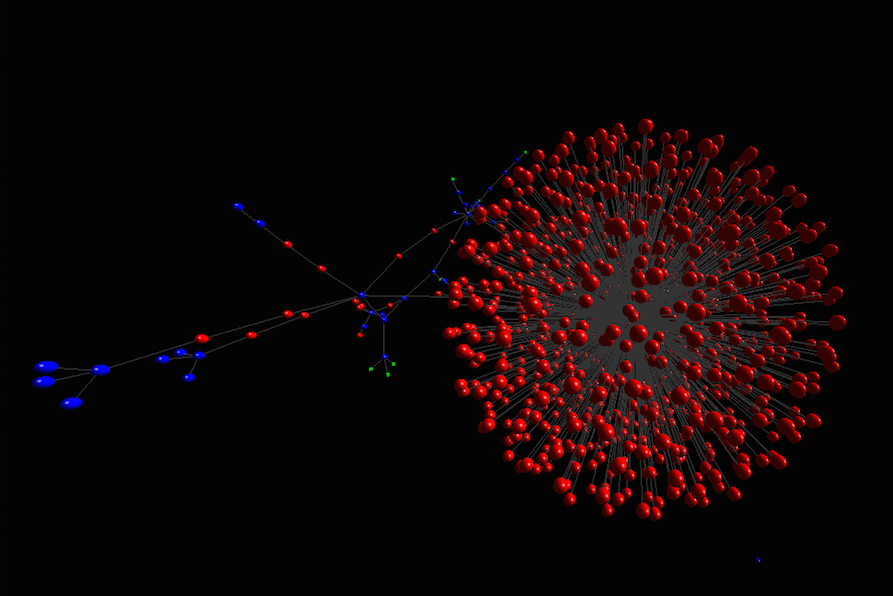
9 run ExLightning.start_linked 5000 which will create 5000 linked processes, which will be linked to the creating process.
Full source code can be found here: https://github.com/holsee/lightning_ex
Have fun :D